不知道题主的“最复杂”是怎么定义的，我假设题主的意思是线段的总长度最长。

于是，最优解如下图所示：

假设相邻两点的距离为 1，那么上图线段的总长度为

证明在文末给出。

另外几个常见的复杂密码包括：

还有下面这个特别常见的：

—–

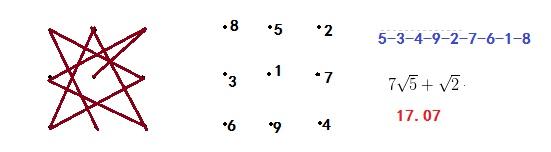
关于线段总长最大为

的证明：

证：

上图已经给出线段总长最大为

的方案 ，我们证明其他的任一方案，都不能使线段总长大于该值。

首先，要使折线总长最大，必然要遍历 9 个点，否则若没有遍历 9 个点，可以继续延长折线到没有经过的点，使总长更大。

于是，折线共分 8 段线段，其中首点和末点连接 1 条线段，其他点各连 2 条线段。

线段的长度从长到短共有以下 5 种：

其中长为 的最多 2 条（2 个对角线）。

1. 数字 1,3,7,9 连出的线段长度可以为

2. 数字 2,4,6,8 连出的线段长度可以为

3. 数字 5 连出的线段长度可以为

① 若数字 5 不为首点或末点

则数字 5 必须连出 2 条线段，长度至多为 ，剩下的 6 条线段至多 2 个 ,4 个 ，于是总长不超过：

（实际上还达不到那么长），所以该情况必然不是最长的。

② 若数字 5 为首点或末点，不妨假设其为首点

理论上来说，首条线段长度至多为 ，剩下 7 段至多有 2 条 ，5 段 ，总长能达到

但仔细分析可知，这种情况是不可能达到的。

如果后面 7 段有 1 段<2，那么总长不超过

故后面 7 段每一段长度都至少为 2（以下分析都基于这个条件）

1. 假设有 2 个长为 的对角线

1.1 假设首条线段长为 （如 5-3）

则第 2 条线段必须长为 （如 5-3-7），否则该对角线没机会再经过了。

第 3 条线段必须长为 （如 5-3-7-6）。由于 1-9 必须连续，该线段的两边可以连 的线段，剩下的 2 段至多长为 2，所以总长至多为

。

1.2 假设首条线段长为 1（如 5-2）

2 个 的对角线的前后两段的长度可以为 ，共 4 个 ，另一条线段长度不超过 2，

总长至多为

2. 假设有 1 个长为 的对角线

总长至多为

（实际上并不能达到，必须要有 1 条不超过 2，总长不超过

）

3. 假设没有长为 的对角线

总长至多为

综上所述，在题设下，线段总长最大为